What is Locality Sensitive Hashing (LSH) ?
Locality Sensitive hashing is a technique to enable creating a hash or putting items in buckets such
- similar items are in the same bucket (same hash) with high probability
- Dissimilar items are in different buckets – i.e dissimilar items are in the same bucket with low probability.
Where is LSH used ? What are some Applications of LSH ?
LSH is used in several applications in data science. Here are some of the popular ways in which LSH is used :
- Nearest Neighbour search: It can be used to implement KNN is a more efficient fashion to efficiently find nearest neighbours – since similar items tend to get the same hash value. KNN is a very popular algorithm that is used in the context of recommendation systems, classification, regression and other ML applications.
- Clustering: Items in the same hash are similar and can be considered to belong to a cluster.
- Dimensionality reduction: The hash value for the item is a lower dimensional representation of the item
- Duplicate detection: Duplicate items will go to the same bucket – can be efficiently detected without comparing with every item in the dataset.
Algorithms based on LSH are used in various domains such as security (digital forencics), anti-spam, digital video finger printing, image and audio similarity and so on..
What are some LSH Implementation Techniques?
There are many algorithms to implement LSH. The popular ones are:
- MinHash: MinHash or the min-wise independant permutations is a popular technique that was originally used for large scale document clustering and eliminating duplicate documents in a search engine.
- Random Projection (SimHash): Based on randomly partitioning the space with hyperplanes to generate hashcodes for items. This is discussed in more detail in the next section.
- Nilsimsa Hash: Is based on generating a hash digest for an email such that the digests of two similar emails are close to each other. It is used in anti-spam applications.
- TLSH : Used for digital forensics to generate the digest of a documents such that similar documents have similar digests. An open source implementation of this algorithm is available.
Digging Deeper into Random Projections for LSH
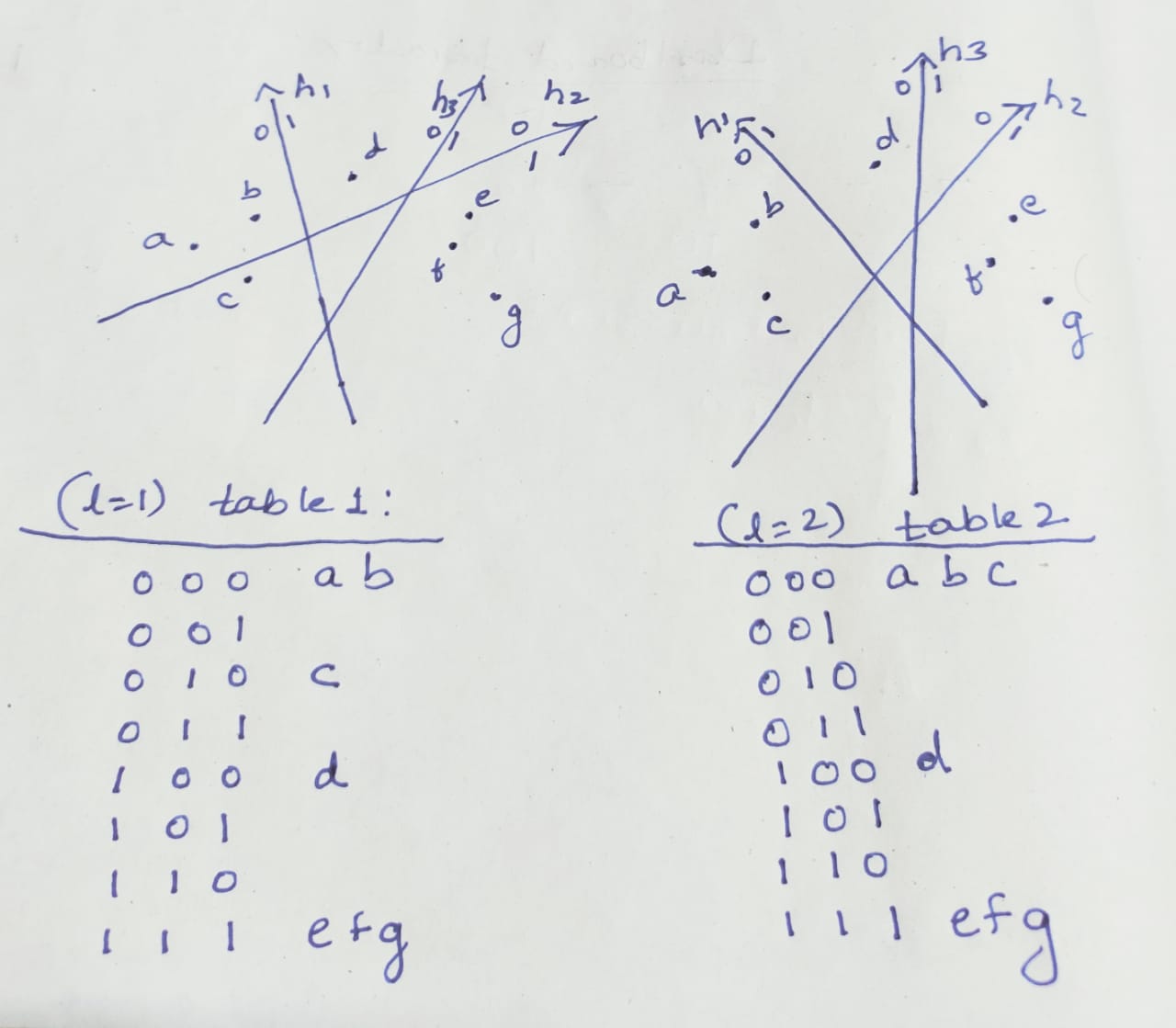
This technique comprises of randomly generating a series of hyperplanes that partition the space. Items lying in the same partition have the same hash value.
Consider a dataset with N points, each with d dimensions.
- Generate a random set of K hyperplanes
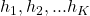
- For every point
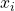 in the dataset (
in the dataset (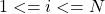 ), generate a hash as follows:
), generate a hash as follows:
- For
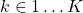
- kth bit of hash = 1 if
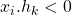
- kth bit of hash = 0 if
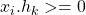
- kth bit of hash = 1 if
- For
To maximize the probability of finding similar items in the same bucket/ same hash, repeat the process L times generating L different sets of K hyperplanes and corresponding hashes for each item. Effectively we have constructed L independant hash tables for the dataset.
Given a point ![]() , in order to retrieve a similar item:
, in order to retrieve a similar item:
- For each repetition (each hash table constructed)
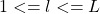
- generate the corresponding hash
- Compare with all other elements in the same bucket of the hash table – add items which are close in value to the output set.
This process is shown in the picture below, how each hash table is constructed based on the space partitioned by the hyper-planes.
How to use LSH in Python ?
https://scikit-learn.org/0.16/modules/generated/sklearn.neighbors.LSHForest.html
The LSHForest module in scikit-learn is a ready implementation of random projections based locality sensitive hashing in python for nearest neighbour search.
Code for TLSH is open-source and available in github:
https://github.com/trendmicro/tlsh
References:
Wiki Article: https://en.wikipedia.org/wiki/Locality-sensitive_hashing
Alexandr Andoni; Indyk, P. (2008). “Near-Optimal Hashing Algorithms for Approximate Nearest Neighbor in High Dimensions”. Communications of the ACM. 51(1): 117–122. CiteSeerX 10.1.1.226.6905. doi:10.1145/1327452.1327494. S2CID 6468963.
Datar, M.; Immorlica, N.; Indyk, P.; Mirrokni, V.S. (2004). “Locality-Sensitive Hashing Scheme Based on p-Stable Distributions”. Proceedings of the Symposium on Computational Geometry.