What is the Dartboard Paradox ?
Assume your are throwing a dart at dartboard such that it hits somewhere on the dartboard. The dartboard paradox: The probability of hitting any specific point on the dartboard is zero. However the probability of hitting somewhere on the dartboard is 1. How can this be ? ( How are the zeros summing up to 1 ? )
What is the resolution to the dartboard paradox?
The dartboard paradox is more of a gap in understanding how probability is defined for a continuous random variable than a paradox. It makes sense to take about probability of the dart hitting a small area in the dart board and not a point. The probability of hitting a given area is non zero, and when integrated across the entire area of the dartboard it is one.
Let us understand this better by first understanding what a pdf is and how it differs from the probability…
What is a Probability Density Function (pdf) for a continuous random variable ?
The probability density function for a given value of random variable X represents the density of probability (probability per unit random variable) within a particular range of that random variable X. It gives us a notion of the relative likelihood of various regions across the range of values the randon variable can take.
An example of a pdf is that for Normal Distribution. 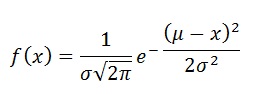
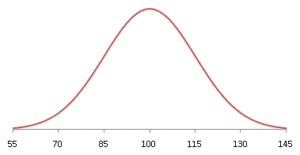 The following are the properties of a pdf:
The following are the properties of a pdf: 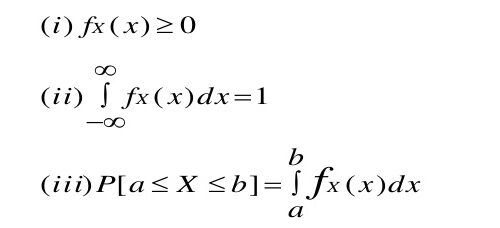
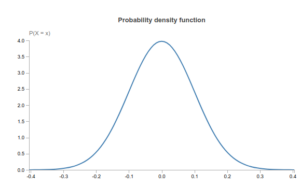
The pdf is always positive, integrates to 1 over the entire support of the random variable. Note however, that there is no upper bound on the value of the pdf. Hecnce the pdf value can be greater than 1. See the example below where we have a normal distrubution with mean 0 and variance 0.1 where the pdf goes well above 4.
The pdf can take a value greater than 1, since it is not really a probability.
What is Probability for a continuous random variable ? How is it didfferent from the pdf ?
The probability can be computed from the pdf by itegrating the pdf over a specific range of the random variable. (This is shown in point ii in the properties of pdf)
When we consider a specific point, it does not have any length (or area in the case of a dartboard). Integrating the pdf over this range gives us a zero! We can instead talk about the probability of the random variable being inbetween a certain small range by integrating the pdf across the range to get a potentially non-zero value.
In the case of the dartboard, there is no paradox when we start talking about the probability of the dart hitting a small area in the dartboard instead of a specific point…