What is the complexity of Viterbi algorithm ?

Viterbi algorithm is a dynamic programming approach to find the most probable sequence of hidden states given the observed data, as modeled by a HMM.
Without dynamic programming, it becomes an exponential problem as there are exponential number of possible sequences for a given observation(How – explained in answer below).
Let the transition probabilities(state transition) be denoted by 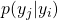$p(y_{j}|y_{i})$ , and the output probabilities be denoted by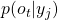 $p(o_{t}|y_{j})$
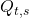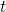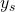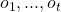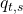Here let us call $Q_{t,s}$ the most probable sequence of hidden states of length $t$ that finishes in the state $y_s$ and generates the output $o_{1},...,o_{t}$ and $q_{t,s}$ be the probability of this sequence which can be computed from the equation below
$q_{t,s}\,=\,max_{k}\,q_{t-1, k}*p(y_s|y_k)*p(o_{t}|y_{s})\,\forall y$

$Q_{t,s}\,=\,argmax_k\,q_{t,k}$
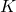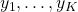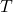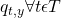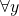Say we have $K$ states $y_1,\hdots,y_K$ , observation sequence of length $T$ , then we need to find $q_{t,y} \forall t \epsilon T$ and $\forall y$ and maximum in each iteration is obtained by checking for all states 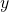$y$ . This leave us with a 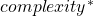$complexity^{*}$ of $O(K^{2}T)$
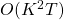
Space complexity: Next question could be what is the extra storage or memory complexity of Viterbi Algorithm –With DP, we always maintain an extra array to store the intermediate computations for reuse to avoid re-work. Here, we maintain a matrix 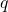$q$ which is $K*T$ in size. We also maintain argmax in every iteration which is also of same size. Hence the memory complexity is $O(K*T)$

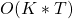
*Hint: To answer such a question one must either remember the exact answer or the algorithm itself. In general, to compute complexity one can check how many times we have terms like “for all” .

Leave a Reply Cancel reply