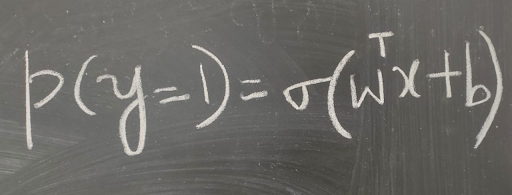Bayesian Logistic Regression
In this video, we try to understand the motivation behind Bayesian Logistic regression and how it can be implemented. 
Recap of Logistic Regression
Logistic Regression is one of the most popular ML models used for classification. It is a generalized linear model where the probability of success can be expressed as a sigmoid of a linear transformation of the features (for binary classification).
Logistic regression is a probabilistic model. Hence, it automatically enables us to compute the probability of success for a new data point as opposed to a hard 0 or 1 for success or failure. A probability of 0.9 can probably be classified as Positive, while a probability of 0.1 can be classified as Negative. A probability of 0.5 implies we cannot take a call.
What we assume here is that we trust the model fully and rely on the probability of success computed from the model for a new point, to take a call.
However, how do we capture the uncertainity about the model itself. How do we know the model parameters themselves are meaningful? How do we know that there was enough data to train the model for instance – that we can rely on the model outcome ?
A small Example
Consider the following example. Suppose we are using Logistic Regression to predict whether a loan can be approved. Suppose we do not train our model on enough data, lets say for arguments sake, we trained our model on just 10 negative examples. Given a new data point, our model is likely to predict the probability of success to be very low (since it overfits on the negative examples).
How do we figure out that we cannot be confidant about this learnt model since we do not have enough data ?
Bayesian Modeling Motivation
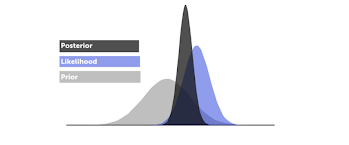
Bayesian Modeling is a paradigm to start with a prior distribution for our parameters. And refine it based on data to learn a posterior distribution. If we see more data, we end up with a peaked posterior that is well refined by the data, else our posterior might be close to the prior when we do not have enough data.
To build models in a Bayesian fashion, it is common to write the *generative process* through which the observed data (in our example the loan approval predictions) are generated.
Inference process involves finding the posterior distribution given the prior and the observed data.
Bayesian Logistic Regression
We can write the generative process for Bayesian Logistic Regression as follows:
 Inference involves finding the posterior distribution of the unknowns given the parameters.
Inference involves finding the posterior distribution of the unknowns given the parameters.
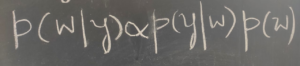 However, the usual way to solve this has been through approximate inference techniques such as variational inference and gibbs sampling with handwritten updates.
However, the usual way to solve this has been through approximate inference techniques such as variational inference and gibbs sampling with handwritten updates.
This can be made easy with tensorflow probability by thinking of logistic regression as a simple feedforward bayesian neural network, where the weights have prior distribution.
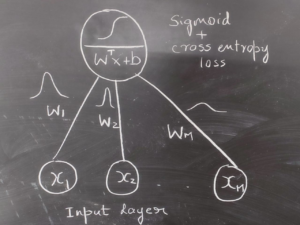 Code for Bayesian Logistic Regression with Tensorflow Probability
Code for Bayesian Logistic Regression with Tensorflow Probability
Check out the following links for an implementation of Bayesian Logistic Regression with tensorflow probability.
https://www.tensorflow.org/probability/overview